Intuition

The problem involves calculating the height of a binary tree after removing subtrees rooted at specific nodes. To efficiently handle multiple queries, we can preprocess the tree to store information about node depths and levels. By leveraging this information, we can quickly determine the new height of the tree after each removal.

Approach

1. Preprocess the Tree:
   • Perform a depth-first search (DFS) to calculate the depth and level of each node.
   • Store this information in a nodeToDepthAndLevel map.
   • Maintain a levelToMaxDepths map to store the two largest depths for each level.
2. Process Queries:
   • For each query:
     • Retrieve the depth and level of the node to be removed.
     • Consult the levelToMaxDepths map to find the two largest depths remaining at that level.
     • Calculate the new height of the tree based on the remaining maximum depths.

Complexity

• Time complexity: O(N + Q), where N is the number of nodes in the tree and Q is the number of queries. The preprocessing DFS takes O(N) time, and each query can be processed in O(1) time.
• Space complexity: O(N), primarily due to the nodeToDepthAndLevel and levelToMaxDepths maps.

Problem

You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.

You have to perform m independent queries on the tree where in the ith query you do the following:

• Remove the subtree rooted at the node with the value queries[i] from the tree. It is guaranteed that queries[i] will not be equal to the value of the root.

Return an array answer of size m where answer[i] is the height of the tree after performing the ith query.

Note:

• The queries are independent, so the tree returns to its initial state after each query.
• The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.

Example 1:

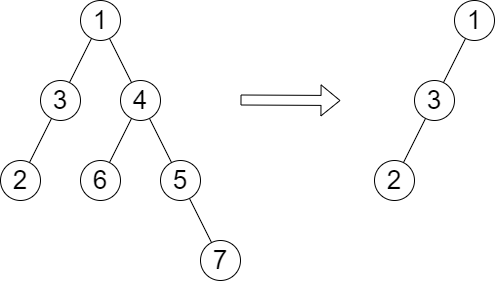
Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
Output: [2]
Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4.
The height of the tree is 2 (The path 1 -> 3 -> 2).

Example 2:

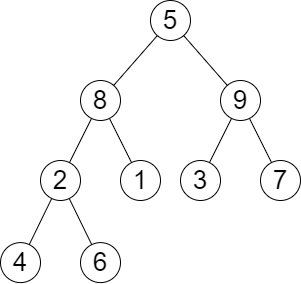
Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
Output: [3,2,3,2]
Explanation: We have the following queries:
- Removing the subtree rooted at node with value 3. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 4).
- Removing the subtree rooted at node with value 2. The height of the tree becomes 2 (The path 5 -> 8 -> 1).
- Removing the subtree rooted at node with value 4. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 6).
- Removing the subtree rooted at node with value 8. The height of the tree becomes 2 (The path 5 -> 9 -> 3).

Constraints:

• The number of nodes in the tree is n.
• 2 <= n <= 105
• 1 <= Node.val <= n
• All the values in the tree are unique.
• m == queries.length
• 1 <= m <= min(n, 104)
• 1 <= queries[i] <= n
• queries[i] != root.val

CodeLeet

Code

PHP

class Solution {
    private $nodeToDepthAndLevel = [];
    private $levelToMaxDepths = [];

    public function treeQueries($root, $queries) {
        $this->traverse($root, 0);

        $result = [];
        foreach ($queries as $query) {
            [$depth, $level] = $this->nodeToDepthAndLevel[$query] ?? [0, 0];
            $maxDepths = $this->levelToMaxDepths[$level] ?? [0, 0];

            $result[] = $level - 1 + max($maxDepths[0], $maxDepths[1] < $depth ? $maxDepths[1] : 0);
        }

        return $result;
    }

    private function traverse($node, $level) {
        if (!$node) {
            return 0;
        }

        $depth = max($this->traverse($node->left, $level + 1), $this->traverse($node->right, $level + 1)) + 1;
        $this->nodeToDepthAndLevel[$node->val] = [$depth, $level];

        $maxDepths = $this->levelToMaxDepths[$level] ?? [0, 0];
        if ($depth > $maxDepths[1]) {
            $maxDepths[0] = $maxDepths[1];
            $maxDepths[1] = $depth;
        } elseif ($depth > $maxDepths[0]) {
            $maxDepths[0] = $depth;
        }
        $this->levelToMaxDepths[$level] = $maxDepths;

        return $depth;
    }
}

GitHub